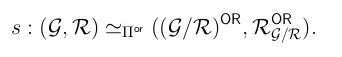Current Work
Projects
Preprints
-
directedTT
Synthetic 1-Categories in Directed Type Theory
— arXiv preprint arXiv:2410.19520
[arXiv page] [pdf] -
paranat
Paranatural Category Theory
— arXiv preprint arXiv:2307.09289
[arXiv page] [pdf]
Talks
-
directedTT
A Type Theory for Synthetic 1-Category Theory
— at the Category Theory Octoberfest 2024, 27 October 2024, online
[Abstract] [Slides] -
paranat
Updates on Paranatural Category Theory
— at the 30th International Conference on Types for Proofs and Programs (TYPES 2024), 11 June 2024, Copenhagen, Denmark
[Abstract] [Slides] -
directedTT
Towards Modal SOGATs
— at the 2024 Meeting of the EuroProofNet Working Group 6, 04 April 2024, Leuven, Belgium
[Abstract] [Blackboard] [Video (YouTube)] -
directedTT
A Sampling of Synthetic 1-Category Theory
— at the Workshop on Homotopy Type Theory/Univalent Foundations, 03 April 2024, Leuven, Belgium
[Abstract] [Slides] [Video (YouTube)] -
paranat
Paranatural Category Theory
— at the Category Theory Octoberfest 2023, 28 October 2023, online
[Abstract] [Slides] [Video] -
paranat
Paranatural Category Theory
— at the CMU HoTT Seminar, 22 September 2023, Pittsburgh, Pennsylvania, USA
[Abstract] [Slides] -
lean-catLogic
Categorical Logic in Lean
— at the 29th International Conference on Types for Proof and Programs (TYPES 2023), 12 June 2023, Valencia, Spain
[Abstract] [Slides] -
directedTT
Presheaf Models of Polarized Higher-Order Abstract Syntax
— at the Second International Conference on Homotopy Type Theory, 24 May 2023, Pittsburgh, USA
[Abstract] [Slides] -
directedTT
The Category Interpretation of (Polarized and Directed) Type Theory
— at the Workshop on Homotopy Type Theory/Univalent Foundations, 23 April 2023, Vienna, Austria
[Abstract] [Slides] [Video (YouTube)] -
paranat
Structural Coends and Bisimulations
— participant talk, Midlands Graduate School, 05 April 2023, Birmingham, UK
[Slides] -
paranat
(Co)ends and (Co)structure
— for HoTT Electronic Seminar Talks (HoTTEST), 01 December 2022, online
[Slides] [Video (YouTube)] -
directedTT
Towards Directed Higher Observational Type Theory
— at the Workshop on Homotopy Type Theory/Univalent Foundations, 01 August 2022, Haifa, Israel
[Abstract] [Slides] -
Groundwork to Higher Allegory Theory
— at the CMU HoTT Seminar, 24 September 2021, Pittsburgh, Pennsylvania, USA
[Slides] -
Allegories and Bisimulations
— at the CMU HoTT Graduate Student Workshop 2021, 26 February 2021, online
[Slides] -
DTL, Refined: Topology, Knowledge, and Nondeterminism
— at the Pittsburgh Formal Epistemology Workshop, 18 July 2021
[Slides] [Details]
Master's Thesis
J. Neumann. Semantics of Nondeterministic Construction. Master's thesis, Carnegie Mellon University, 2020.
Slides from thesis defense
My master's thesis combines insights from modal logic, formal epistemology, and theoretical computer science into a mathematically-ambitious analysis of a very simple activity: flipping a coin. Based on an insight by my thesis advisor, Adam Bjorndahl, I develop dynamic topological logic as a suitable language for formally articulating and reasoning about the capacities of knowledgeable agents in situations where nondeterministic actions are possible. I focus on situations where our agent is able to flip a coin to choose between two possible courses of action, and rigorously examine how the uncertainty created by the coin interacts with the agent's capacity for knowledge.
This work is primarily focused on the model theory of dynamic topological logic: "equipping the agent with a coin to flip" corresponds mathematically to a kind of transformation of dynamic topological structures, which I call a program constructor. To fully elucidate the theory of program constructors requires extensive mathematical development, including the introduction of several novel notions in the theory of dynamic topological models and frames. Along the way, I develop a deep connection between program construction in the dynamic topological setting, and analogous processes in the relational model theory of propositional dynamic logic. Though this thesis leaves much work to be done, it establishes a robust framework for future exploration of this very rich topic.